Home page > Archives 2005-2006-2007 > 2007 Spring Summer
school : Conners Emerson School
city : Bar Harbor
country : Maine USA
address :
postal code :
latitude : 44°23 N = 44.383°
longitude : 68°13’ W = -68.227°
year : 2007
44,39°N 68,21°W
meter stick 100 cm
20/03/2007
shadow 94.0 cm 43,2°
 Our school is called Conners-Emerson. It is a K-8 school. We are in fifth grade reading Gifted. We live on an island of the coast of Maine. It’s location is lat. 44.39 N and long. 68.21W.
Our school is called Conners-Emerson. It is a K-8 school. We are in fifth grade reading Gifted. We live on an island of the coast of Maine. It’s location is lat. 44.39 N and long. 68.21W.
To figure out the circumference of the Earth, we figured out when high noon would be on the Equinox and at that time we got together with our sun-shadow apparatus and watched the shadow until it got as short as it would. To see a picture of us, and a diagram we made of our apparatus, please go to our school gt website: http://blue1.emerson.u98.k12.me.us/...
If we could do anything differently then, we would have made our meter stick steadier because it wasn’t at a right angle. It was a really windy day, and the wind really made it hard to keep the stick vertical. We learned that if you are a few degrees off, the measurements are really a few thousand kilometers off.
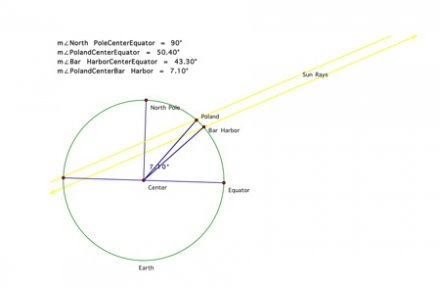 To find the circumference of the Earth, our calculations looked like this:
To find the circumference of the Earth, our calculations looked like this:
1. Our Sun Angle (44.00) minus Fox Focus’ Sun Angle (34.25) equals 9.75°
2. To find the North-South distance we subtracted Our Latitude (44.39N) minus Fox Focus’ Latitude (34.01N) which equals 10.38. Because we know that 1° equals 111 km, we multiplied the difference in latitude (10.38°) by 111 and got 1152.18 km, our North-South distance.
3. Then (remember the Sun angles?) we divided 360° by the difference of Fox Focus’ Sun Angle and Our Sun Angle (9.75°). Multiply that by 1152.18 km, and you get the Earth’s circumference, 42531.84 km!!!
4. The difference between our measurement and the real circumference is 2,466 km
 The main idea of this project was to find the circumference of the Earth by ourselves, using trigonometry. This Project was chosen for us so that we could apply the math skills that we were learning (trig), and to use what we were learning in a real life situation. We had already studied right triangle trigonometry in class a little earlier in the year, so this made the project a little easier.
The main idea of this project was to find the circumference of the Earth by ourselves, using trigonometry. This Project was chosen for us so that we could apply the math skills that we were learning (trig), and to use what we were learning in a real life situation. We had already studied right triangle trigonometry in class a little earlier in the year, so this made the project a little easier.
To do this, the procedure was quite intricate, but we managed to come pretty close to the actual circumference of our Earth. For our final measurement of the circumference of the Earth we got 40,039.6 km. This is very close to the actual measurement of the Earth, which is 40,066 km.
The first thing that we had to do was to find out when true noon was on the day of the Spring Equinox. The Equinox, for those who do not know, is the first day of spring, when the day has the same length as the night. We found that we would have to measure the length of the sun’s shadow at 12:41 pm.
To help us with this, we made a contraption out of a board and a bookend that would help us keep a meter stick at a 90˚ angle. When the sun’s rays were coming in, the meter stick would cast a shadow. At noon, we measured the distance of the shadow and marked it down onto the attached board. Then we went back into our classroom and attached one end of a piece of string to the tip of the meter stick and then attached the other end to the mark of our shadow. Using right triangle trigonometry, we were able to find the angle of the sun to our latitude (the angle that had our shadow mark as a vertex), since we knew that the meter stick formed a 90º angle with the board and we had two side lengths (the length of the meter stick, and the length from the base of the meter stick to our shadow mark, which we measured using a measuring tape). This was a relatively simple process since we had already been studying trig in class.
After this we had to find the difference between our sun angle and our partner school in Poland’s sun angle. This equaled 7.2 degrees, and was our central angle, or the angle from the center of the Earth to our two latitudes.
For our next step we found out what our distance (latitude wise) was from the Polish school. This equaled 674 km.
We found this two ways. The first way we did this was to use a web site that allowed you to type in two long/lat positions and then it would tell you the distance. Since we didn’t want the actual distance between our town and Poland, we changed Poland’s long/lat position so that they were on the same longitude as us and then had the web site calculate the distance. The second way that we found this information was to calculate it ourselves using the ratio that 1º latitude =111 km. So since we knew the central angle between us and Poland we were able to use this method as a way to check the other calculations.
Our last step, now that we had all the appropriate information, was to actually calculate the circumference of the Earth. We knew that 7.2 degrees was to 360 degrees (the measure of a full circle) as 674 km was to the circumference of the Earth, x. So we set this up as a proportion and solved for x. We got 40,039.6 km, and knew this was the rough circumference. Our calculations had a 1% error rate from the actual circumference.
 Although this measurement is very close to the actual measurement of the Earth’s circumference, there are many places in this procedure where we could have made an error. There are many natural errors that could have occurred. Our main place of error was most likely when we took the measure of the meter stick’s shadow. Since the wind was blowing rather hard it is likely that our contraption was not as steady as it should have been, making our measurement off. However, the wind was not the only thing that could have factored an error into our equation. Because the ground which we took our measurement from was not a completely flat surface the board was not completely still, and our measurement was not as accurate as it could have been.
Although this measurement is very close to the actual measurement of the Earth’s circumference, there are many places in this procedure where we could have made an error. There are many natural errors that could have occurred. Our main place of error was most likely when we took the measure of the meter stick’s shadow. Since the wind was blowing rather hard it is likely that our contraption was not as steady as it should have been, making our measurement off. However, the wind was not the only thing that could have factored an error into our equation. Because the ground which we took our measurement from was not a completely flat surface the board was not completely still, and our measurement was not as accurate as it could have been.
We think that this was a good experience for us. It gave us an opportunity to realize how people apply the techniques and skills that we are learning in geometry in real life situations. I think that by doing things outside of the classroom we can get a better understanding and a better feel for how to use them. Doing this is a way that we can be more confident, and more apt at mathematics in the future. To see a diagram that we have made and a picture of our class click the link below :
![]() en
en
![]() Archives 2005-2006-2007
Archives 2005-2006-2007
![]() 2007 Spring Summer
?
2007 Spring Summer
?





